Le contenu de ce site est diffusé sous licence Creative Commons Paternité- Pas d'utilisation commerciale Canada

Table des matières A B C D E     Imprimer L'EXPÉRIMENTATION B1 B2 B3 B4 B5 B6 B7 B8 B8 - L'évaluation de l'incertitude Sommaire 1. Introduction 2. Incertitude associée à la précision limitée du processus de mesure 3. Incertitude associée à la mauvaise définition ou à l'instabilité de l'objet mesuré (incertitude définitionnelle) 4. Exemple    [ sommaire ] [ suivant ] 1. Introduction Comme il est expliquée dans le texte B7, les méthodes employées pour déterminer l'incertitude diffèrent selon que celle-ci provient de la mauvaise définition ou de l'instabilité de l'objet (incertitude définitionnelle) ou de la précision limitée du processus de mesure (incertitude de mesure). Dans les deux cas, la nature de ces méthodes permet de distinguer deux types d'incertitude. - Incertitude de type A. Lorsque plusieurs mesures individuelles successives dans les mêmes conditions fournissent des valeurs différentes, réparties autour de la vraie valeur de la caractéristique. L'incertitude est alors obtenue par un calcul statistique fondé sur ces valeurs individuelles. - Incertitude de type B. Lorsque l'incertitude est évaluée de toute autre façon, de manière plus ou moins subjective.    [ sommaire ] [ précédent ] [ suivant ] 2. Incertitude associée à la précision limitée du processus de mesure On suppose ici que la caractéristique mesurée est stable et bien définie, de sorte que l'incertitude provient principalement de la précision limitée du processus de mesure. Deux cas de figure se présentent. a) Mesure fournissant une valeur unique (incertitude de type B) Dans ce cas, il s'agit d'évaluer, au meilleur de notre jugement et en nous fondant sur nos connaissances tant de l'objet que du processus de mesure, dans quel éventail (entre des valeurs minimale et maximale, vmin et vmax) on est à peu près certain que se situe la valeur de la caractéristique que l'on mesure. Il s'agit certes d'une procédure subjective. L'incertitude est alors définie comme la moitié de la fourchette, et la valeur de la caractéristique s'exprime comme suit : valeur centrale ± moitié de l'éventail soit, mathématiquement : 1/2 (vmin + vmax)  ±  1/2 (vmax − vmin) (B8.1) Ainsi, une expression telle que 2,34 ± 0,02 cm signifie qu'on est à peu près certain que la quantité que l'on mesure vaut entre 2,32 et 2,36 cm ou, autrement dit, qu'il est fort peu probable qu'elle vaille 2,31 cm et moins, ou 2,37 cm et plus. Pour les mesures de type analogique, c'est-à-dire celles qui font intervenir la position d'un repère sur une échelle graduée, il n'existe pas de règle universelle; il faut à chaque fois se poser la question et y répondre en fonction de ce qu'on observe. On lit parfois dans des ouvrages sur le sujet que l'incertitude est égale à la moitié de la plus petite division, mais l'expérience montre que cela n'est pas toujours le cas. Bien souvent, on peut lire jusqu'au quart de la plus petite division, ou même plus précisément encore, alors que dans des dans conditions d'utilisation adverses, il se peut qu'on ne puisse même pas atteindre la précision de la plus petite division. La situation est différente pour les affichages numériques, où il est vrai que la moitié de l'unité la plus petite (ou la résolution) de l'appareil, constitue une estimation raisonnable de l'incertitude. Par exemple, une valeur de 5,34 V (volts) affichée de manière stable, donc une résolution de 0,01 V, peut être interprétée comme se situant entre 5,335 V et 5,345 V, ce qui s'écrit 5,34 ± 0,005 V. Le mode d'emploi d'un appareil qui affiche des valeurs, que ce soit de façon numérique ou par un dispositif analogique (aiguille ou autre), indique généralement la précision qu'il procure. Cette précision est parfois donnée en pourcentage, ou une combinaison d'une constante et d'un pourcentage, et peut varier selon la plage de valeurs considérée. Ainsi, l'incertitude sera donnée par la plus grande des valeurs suivantes : - la valeur estimée comme décrit ci-dessus (en général, la moitié de la résolution de l'appareil); - la précision indiquée dans le mode d'emploi de l'appareil. Note Comme les incertitudes ainsi obtenues sont des estimations « à vue de nez », elles ne sont habituellement exprimées qu'avec un seul chiffre significatif. On peut cependant employer les formes ± 0,15 et ± 0,25, qu'on peut considérer comme possédant en quelque sorte un chiffre significatif et demi. Cependant, des valeurs comme ± 0,125 ou ± 0,35 seront de préférence arrondies à un seul chiffre significatif, soit ± 0,1 et ± 0,4, respectivement. Cependant, lorsque l'incertitude provient d'un calcul (écart-type, notamment) fondé sur un grand nombre de mesures, on peut afficher sa valeur avec deux chiffres significatifs. Ainsi, l'incertitude sur les valeurs des constantes fondamentales (voir, par exemple, Taylor et Mohr), mesurées à l'aide de méthodes sophistiquées, comprend souvent deux chiffres significatifs. Notez que cette valeur est parfois indiquée entre parenthèses au lieu d'être précédée du symbole ±. Pour des explications et des consignes sur les chiffres significatifs et l'arrondissement des nombres, consultez le document suivant (dans une nouvelle fenêtre). Cas particulier : mesure en bloc d'un groupe d'objets identiques Lorsqu'on a de très bonnes raisons de croire que la valeur d'une caractéristique d'un objet fabriqué en série, ou encore d'un phénomène répétitif, varie très peu d'un spécimen ou d'une occurrence à l'autre (en comparaison de la précision du processus de mesure), on peut réduire l'incertitude estimée en mesurant en bloc un certain nombre de spécimens. L'incertitude sur la valeur obtenue (qui est la valeur totale mesurée divisée par le nombre de spécimens) est alors divisée par ce même nombre. Autrement dit, avec une règle affectée d'une incertitude de 0,5 mm, on obtient une incertitude de 0,05 mm si on mesure 10 objets en bloc, en les mettant bout à bout, si l'on suppose bien sûr que leurs dimensions varient beaucoup moins que 0,05 mm d'un spécimen à l'autre. Cette méthode a donc une limite : si on accroît le nombre de spécimens, l'incertitude diminuera au point de devenir comparable à la variation de la valeur d'un spécimen à l'autre. Un appareil plus précis et des méthodes statistiques (voir plus loin) doivent alors être employés pour effectuer des mesures individuelles et en tirer la véritable valeur de l'incertitude, qui traduira (par un intervalle de confiance à 95 %) cette variation entre les spécimens. b) Mesure combinant une série de mesures individuelles (type A) On a vu dans le texte B7 que lorsque la valeur d'une caractéristique est obtenue à partir d'un très grand nombre de mesures individuelles, la vraie valeur (valeur centrale) est la moyenne de ces mesures. Plus le nombre de mesures est élevé, plus la moyenne tend à se rapprocher de cette valeur (voir, dans une nouvelle fenêtre, la figure 5 du texte B7). Selon les lois de la statistique, pour que la fourchette d'incertitude ait une probabilité de 95 % de comprendre la vraie valeur, l'incertitude doit être prise comme le double de l'écart-type de l'ensemble des valeurs, divisé par la racine carrée du nombre de mesures. Le résultat de l'opération de mesure peut donc s'exprimer comme suit  :    (B8.2) On constate que si on augmente le nombre de mesures, l'incertitude diminue. Toutefois, celle-ci ne peut être inférieure à la résolution de l'appareil de mesure.    [ sommaire ] [ précédent ] [ suivant ] 3. Incertitude associée à la mauvaise définition ou à l'instabilité de l'objet mesuré (incertitude définitionnelle) On suppose ici que le processus de mesure est d'une grande précision, et que l'incertitude provient principalement de la mauvaise définition ou de l'instabilité de l'objet. Deux cas de figure se présentent. a) Mesures exhaustives (incertitude de type B) Cela correspond aux deux situations suivantes : - on a mesuré uniquement les valeurs extrêmes possibles, en excluant éventuellement les valeurs aberrantes; - les valeurs possibles sont en nombre restreint (moins d'une dizaine) et ont toutes été mesurées. On définit simplement la valeur et son incertitude de manière à couvrir l'éventail complet de ces valeurs. Ainsi, la valeur est la moyenne des mesures extrêmes (vmin et vmax) et l'incertitude la moitié de l'écart entre ces extrêmes, comme dans la formule B8.1 : 1/2 (vmin + vmax)  ±  1/2 (vmax − vmin) Note. L'incertitude est de type B même si dans la seconde situation on disposait d'un ensemble de mesures individuelles, car on ne les a pas utilisées pour calculer les caractéristiques de la distribution des valeurs possibles. On a plutôt supposé a priori que toutes les valeurs étaient également probables (distribution uniforme).    b) Mesures formant un échantillon des valeurs possibles (incertitude de type A) Les valeurs obtenues forment un échantillon des valeurs possibles de la caractéristique mesurée, valeurs très nombreuses dont l'étendue de l'éventail est inconnue. Comme en 2b, la moyenne des valeurs mesurées donne une très bonne idée de la vraie valeur, celle-ci étant définie comme la moyenne d'un nombre infini de mesures. Plus le nombre de mesures est élevé, plus cette moyenne tend à se rapprocher de la vraie valeur. De son côté, l'écart-type de l'ensemble des valeurs fournit une bonne idée de l'éventail des valeurs possibles. Pour que la fourchette formée par l'incertitude corresponde à environ 95 % de cet éventail (intervalle de confiance à 95 %), l'incertitude doit être prise comme le double de l'écart-type de l'ensemble des valeurs. Dès qu'on dispose d'un certain nombre de mesures individuelles (environ 10~15), il devient peu utile d'en accumuler davantage. La moyenne des valeurs est alors suffisamment proche de la vraie valeur, et l'incertitude ne changerait plus de manière notable si on augmentait le nombre de mesures. Le résultat de la mesure s'exprime alors comme suit : moyenne  ±  2 × écart-type (B8.3) Note. Il se peut que l'obtention d'un très grand nombre de mesures révèle que la distribution des valeurs est telle que la formule B8.3 ne correspond plus à un intervalle de confiance à 95 %. L'étude de ces situations fait cependant appel à des notions avancées de statistiques. La distribution donnant lieu à la formule B8.3 (distribution normale) est cependant celle qui survient le plus souvent. Le tableau suivant présente, dans une nouvelle fenêtre, une synthèse des explications du texte B7 et du présent texte.    [ sommaire ] [ précédent ] 4. Exemple En guise d'illustration, supposons que 20 mesures individuelles de tension électrique, à l'aide d'un voltmètre dont la résolution est 0,02 V, donnent une moyenne de 12,336 V avec un écart-type de 0,172 V. La valeur T de la tension résultant de cet ensemble de mesures sera alors donnée, avec un intervalle de confiance de 95 %, par (remarquez la manière dont les valeurs ont été arrondies) : - T  =  12,34 ± 0,08 V, si on a de bonnes raisons de croire que le voltage était très stable, mais que c'est le manque de fidélité de l'appareil qui causait les différences d'une mesure à l'autre. 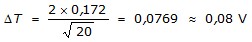Dans ce cas, on emploie B8.2 : en vérifiant que cette valeur est beaucoup plus grande que la moitié de la résolution de l'appareil (0,01 V). - T  =   12,3 ± 0,3 V, si l'on sait que l'appareil est d'une bonne précision, et donc que les diverses valeurs mesurées correspondaient à des fluctuations dans le voltage lui-même. Dans ce cas, c'est plutôt B8.3 qui s'applique : ΔT  =   2 × 0,172  =  0,344  ≈  0,3 V    Notons que dans les deux cas il s'agit d'une incertitude de type A.   [ début ]